K-means算法属于无监督学习聚类算法,其计算步骤还是挺简单的,思想也挺容易理解,而且还可以在思想中体会到EM算法的思想。
K-means 算法的优缺点:
1.优点:容易实现
2.缺点:可能收敛到局部最小值,在大规模数据集上收敛较慢
使用数据类型:数值型数据
以往的回归算法、朴素贝叶斯、SVM等都是有类别标签y的,因此属于有监督学习,而K-means聚类算法只有x,没有y
在聚类问题中,我们的训练样本是
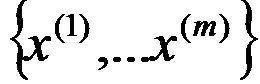
其中每个Xi都是n维实数。
样本数据中没有了y,K-means算法是将样本聚类成k个簇,具体算法如下:
1、随机选取K个聚类质心点,记为
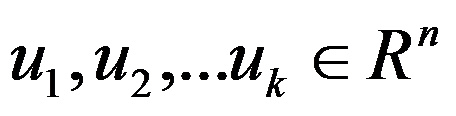
2、重复以下过程直到收敛
{
对每个样例 i ,计算其应该属于的类:
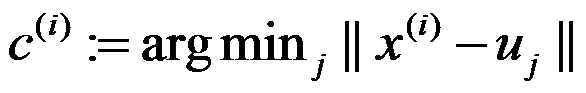
对每个类 j ,重新计算质心:
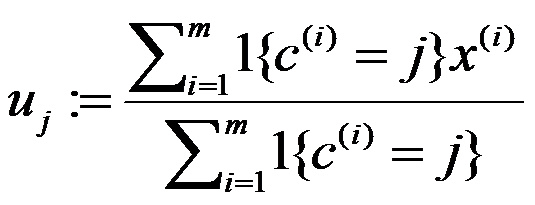
}
其中K是我们事先给定的聚类数目,Ci 表示样本 i 与K个聚类中最近的那个类,Ci的值是1到K中的一个,质心uj代表我们对属于同一个类的样本中心的猜测。解释起来就是,
第一步:天空上的我们随机抽取K个星星作为星团的质心,然后对于每一个星星 i,我们计算它到每一个质心uj的距离,选取其中距离最短的星团作为Ci,这样第一步每个星星都有了自己所属于的星团;
第二步:对每个星团Ci,我们重新计算它的质心uj(计算方法为对属于该星团的所有点的坐标求平均)不断重复第一步和第二步直到质心变化很小或者是不变。
然后问题来了,怎么样才算质心变化很小或者是不变?或者说怎么判定?答案就是畸变函数(distortion function),定义如下:
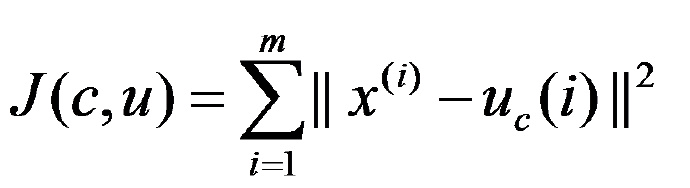
J函数表示每个样本点到其质心的距离平方和,K-means的收敛就是要将 J 调整到最小,假设当前 J 值没有达到最小值,那么可以先固定每个类的质心 uj ,调整每个样例的类别 Ci 来时 J 函数减少。同样,固定 Ci ,调整每个类的质心 uj也可以是 J 减少。这两个过程就是内循环中使 J 单调变小的过程。当 J 减小到最小的时候, u 和 c 也同时收敛。(该过程跟EM算法其实还是挺像的)理论上可能出现多组 u 和 c 使 J 取得最小值,但这种情况实际上很少见。
由于畸变函数 J 是非凸函数,所以我们不能保证取得的最小值一定是全局最小值,这说明k-means算法质心的初始位置的选取会影响到最后最小值的获取。不过一般情况下,k-means算法达到的局部最优已经满足要求。如果不幸代码陷入局部最优,我们可以选取不同的初始值跑多几遍 k-means 算法,然后选取其中最小的 J 对应的 u 和 c 输出。
另一种收敛判断:
实际我们编写代码的时候,还可以通过判断“每个点被分配的质心是否改变”这个条件来判断聚类是否已经收敛
而上面所说的畸变函数则可以用来评估收敛的效果,具体将会在下面的实例中体现。
Matlab 实现
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
|
function kMeansclcclearK = 4;dataSet = load('testSet.txt');[row,col] = size(dataSet);% 存储质心矩阵centSet = zeros(K,col);% 随机初始化质心for i= 1:col minV = min(dataSet(:,i)); rangV = max(dataSet(:,i)) - minV; centSet(:,i) = repmat(minV,[K,1]) + rangV*rand(K,1);end% 用于存储每个点被分配的cluster以及到质心的距离clusterAssment = zeros(row,2);clusterChange = true;while clusterChange clusterChange = false; % 计算每个点应该被分配的cluster for i = 1:row % 这部分可能可以优化 minDist = 10000; minIndex = 0; for j = 1:K distCal = distEclud(dataSet(i,:) , centSet(j,:)); if (distCal < minDist) minDist = distCal; minIndex = j; end end if minIndex ~= clusterAssment(i,1) clusterChange = true; end clusterAssment(i,1) = minIndex; clusterAssment(i,2) = minDist; end% 更新每个cluster 的质心 for j = 1:K simpleCluster = find(clusterAssment(:,1) == j); centSet(j,:) = mean(dataSet(simpleCluster',:)); endendfigure%scatter(dataSet(:,1),dataSet(:,2),5)for i = 1:K pointCluster = find(clusterAssment(:,1) == i); scatter(dataSet(pointCluster,1),dataSet(pointCluster,2),5) hold onend%hold onscatter(centSet(:,1),centSet(:,2),300,'+')hold offend% 计算欧式距离function dist = distEclud(vecA,vecB) dist = sqrt(sum(power((vecA-vecB),2)));end |
效果如下:
这是正常分类的情况,很明显被分为了4个类,不同颜色代表不同的类,cluster的质心为 “ + ”
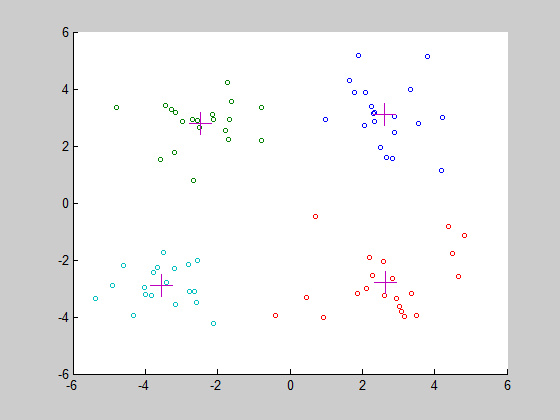
当然,这只是其中一种情况,很有可能我们会出现下面这种情况:
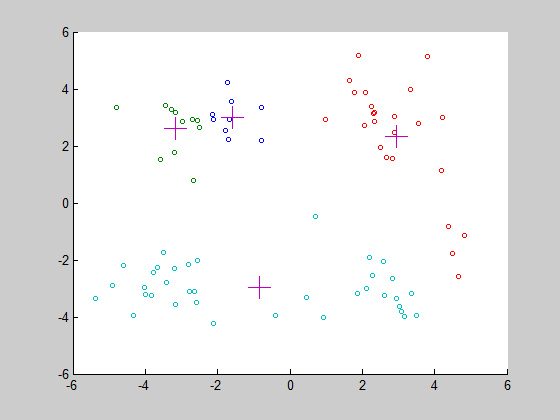
这就是上面所说的,K-means的缺点之一,随机初始点的选择可能会让算法陷入局部最优解,这时候我们只需重新运行一次程序即可。
至于每一个看似都可以正常聚类的情况呢,我们则利用上面所说的“畸变函数”来衡量聚类的效果,当然是J越小聚类效果越好。
实际使用的时候,我们只需多次运行程序,选取J最小的聚类效果。
转自 http://blog.jobbole.com/86909/
 3G Eden
3G Eden RSS
RSS