KNN 算法其实简单的说就是“物以类聚”,也就是将新的没有被分类的点分类为周围的点中大多数属于的类。它采用测量不同特征值之间的距离方法进行分类,思想很简单:如果一个样本的特征空间中最为临近(欧式距离进行判断)的K个点大都属于某一个类,那么该样本就属于这个类。这就是物以类聚的思想。
当然,实际中,不同的K取值会影响到分类效果,并且在K个临近点的选择中,都不加意外的认为这K个点都是已经分类好的了,否则该算法也就失去了物以类聚的意义了。
KNN算法的不足点:
1、当样本不平衡时,比如一个类的样本容量很大,其他类的样本容量很小,输入一个样本的时候,K个临近值中大多数都是大样本容量的那个类,这时可能就会导致分类错误。改进方法是对K临近点进行加权,也就是距离近的点的权值大,距离远的点权值小。
2、计算量较大,每个待分类的样本都要计算它到全部点的距离,根据距离排序才能求得K个临近点,改进方法是:先对已知样本点进行剪辑,事先去除对分类作用不大的样本。
适用性:
适用于样本容量比较大的类域的自动分类,而样本容量较小的类域则容易误分
算法描述:
1、计算已知类别数据集合汇总的点与当前点的距离
2、按照距离递增次序排序
3、选取与当前点距离最近的K个点
4、确定距离最近的前K个点所在类别的出现频率
5、返回距离最近的前K个点中频率最高的类别作为当前点的预测分类
Python 实现
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
from numpy import *import operatordef createDataSet(): group = array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]]) lables = ['A','A','B','B'] return group,lables# KNN 分类算法def classify0(inx,dataSet,labels,k): dataSetSize = dataSet.shape[0] # shape[0]获取行 shape[1] 获取列 # 第一步,计算欧式距离 diffMat = tile(inx,(dataSetSize,1)) - dataSet #tile类似于matlab中的repmat,复制矩阵 sqDiffMat = diffMat ** 2 sqDistances = sqDiffMat.sum(axis=1) distance = sqDistances ** 0.5 sortedDistIndecies = distance.argsort() # 增序排序 classCount = {} for i in range(k): # 获取类别 voteIlabel = labels[sortedDistIndecies[i]] #字典的get方法,查找classCount中是否包含voteIlabel,是则返回该值,不是则返回defValue,这里是0 # 其实这也就是计算K临近点中出现的类别的频率,以次数体现 classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1 # 对字典中的类别出现次数进行排序,classCount中存储的事 key-value,其中key就是label,value就是出现的次数 # 所以key=operator.itemgetter(1)选中的事value,也就是对次数进行排序 sortedClassCount = sorted(classCount.iteritems(),key=operator.itemgetter(1),reverse=True) #sortedClassCount[0][0]也就是排序后的次数最大的那个label return sortedClassCount[0][0] |
调用方式:
|
1
2
3
4
5
6
|
import sys;sys.path.append("/home/llp/code/funcdef")import KNNgroup,labels = KNN.createDataSet();relust = KNN.classify0([0,0],group,labels,3)print 'the classify relust is :' , relust |
Matlab 实现
这里以一个完整实例呈现,代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
|
function relustLabel = KNN(inx,data,labels,k)%%% inx 为 输入测试数据,data为样本数据,labels为样本标签%%[datarow , datacol] = size(data);diffMat = repmat(inx,[datarow,1]) - data ;distanceMat = sqrt(sum(diffMat.^2,2));[B , IX] = sort(distanceMat,'ascend');len = min(k,length(B));relustLabel = mode(labels(IX(1:len)));end |
可以看到,整个KNN算法的Matlab代码也就只有6行,比Python少很多,这其中要得益于Matlab成熟的矩阵计算和很多成熟的函数。
实际调用中,我们利用一个数据集进行测试,该数据集是由1000个样本的3维坐标组成,共分为3个类
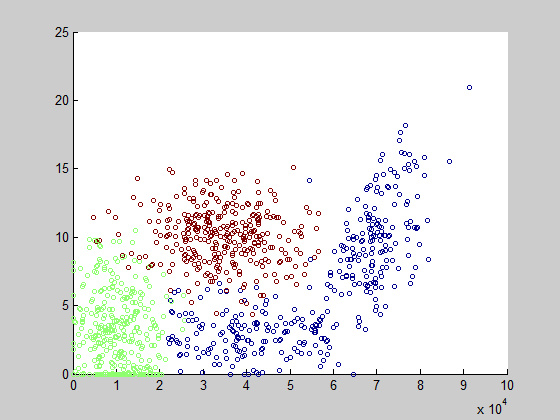
首先可视化我们的数据集,看看它的分布:
第一维和第二维:可以清晰地看到数据大致上分为 3 类
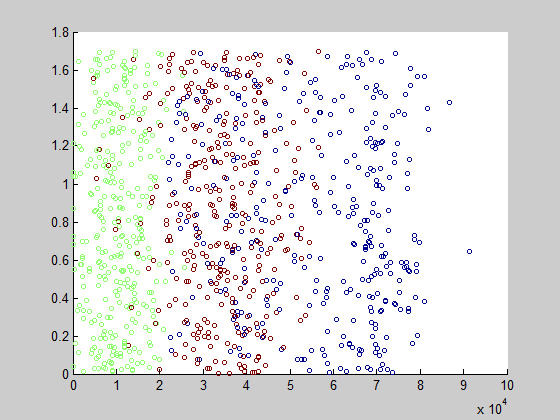
第1维和第3维:从这个角度看,3类的分布就有点重叠了,这是因为我们的视角原因
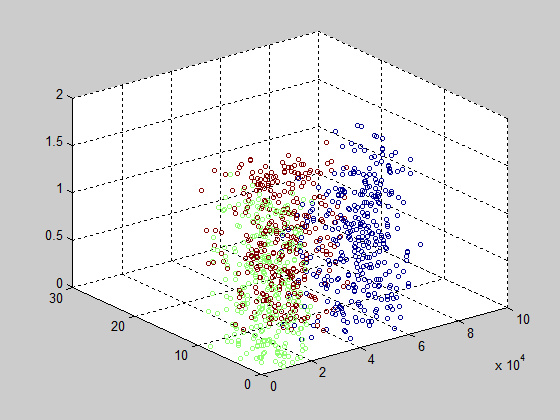
画出3维,看看它的庐山真面目:
由于我们已经编写了KNN代码,接下来我们只需调用就行。了解过机器学习的人都应该知道,很多样本数据在代入算法之前都应该进行归一化,这里我们将数据归一化在[0,1]的区间内,归一化方式如下:
newData = (oldData-minValue)/(maxValue-minValue)
其中,maxValue为oldData的最大值,minValue为 oldData 的最小值。
同时,我们对于1000个数据集,采取10%的数据进行测试,90%的数据进行训练的方式,由于本测试数据之间完全独立,可以随机抽取10%的数据作为测试数据,代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
function KNNdatgingTest%%clcclearclose all%%data = load('datingTestSet2.txt');dataMat = data(:,1:3);labels = data(:,4);len = size(dataMat,1);k = 4;error = 0;% 测试数据比例Ratio = 0.1;numTest = Ratio * len;% 归一化处理maxV = max(dataMat);minV = min(dataMat);range = maxV-minV;newdataMat = (dataMat-repmat(minV,[len,1]))./(repmat(range,[len,1]));% 测试for i = 1:numTest classifyresult = KNN(newdataMat(i,:),newdataMat(numTest:len,:),labels(numTest:len,:),k); fprintf('测试结果为:%d 真实结果为:%d\n',[classifyresult labels(i)]) if(classifyresult~=labels(i)) error = error+1; endend fprintf('准确率为:%f\n',1-error/(numTest))end |
当我们选择K为4的时候,准确率为:97%
KNN进阶
接下来我们将运用KNN算法实现一个手写识别系统,训练数据集大约2000个样本,每个数字大概有200个样本
测试数据大概有900个样本,由于每个样本都是一个32×32的数字,我们将其转换为1×1024的矩阵,方便我们利用KNN算法
数据如下:

由于数据量比较大,加载数据的时候回花一点时间,具体代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
function handWritingTest%%clcclearclose all%% 获取目录下的所有txt文件名称d = dir(['digits/trainingDigits/' '*.txt']); % struct 类型dircell = struct2cell(d); %cell 类型trainSetLen = size(dircell,2);K = 4;dataSize = 1024;trainLabels = zeros(trainSetLen,1);trainSet = [];simpleTrainSet = zeros(1,dataSize);simpleTestSet = zeros(1,dataSize);%% 加载数据fprintf('loading data...')for i = 1:trainSetLen trainName = dircell(1,i); trainFilename = cell2mat(trainName); trainLabels(i) = str2num(trainFilename(1));fid = fopen(['digits/trainingDigits/' trainFilename],'r'); traindata = fscanf(fid,'%s'); for j = 1:dataSize simpleTrainSet(j) = str2num(traindata(j)); end trainSet = [trainSet ; simpleTrainSet]; fclose(fid);endd = dir(['digits/testDigits/' '*.txt']); % struct 类型dircell = struct2cell(d); %cell 类型testSetLen = size(dircell,2);error = 0;%% 测试数据for k = 1:testSetLen testName = dircell(1,k); testFilename = cell2mat(testName); testLabels = str2num(testFilename(1));fid = fopen(['digits/testDigits/' testFilename],'r'); testdata = fscanf(fid,'%s'); for j = 1:dataSize simpleTestSet(j) = str2num(testdata(j)); end classifyResult = KNN(simpleTestSet,trainSet,trainLabels,K); fprintf('识别数字为:%d 真实数字为:%d\n' , [classifyResult , testLabels]) if(classifyResult~=testLabels) error = error+1; end fclose(fid);endfprintf('识别准确率为:%f\n',1-error/testSetLen)end |
不同的K识别准确率稍有不同,当K为4的时候,准确率为 98.31%
转自 http://blog.jobbole.com/86901/
 3G Eden
3G Eden RSS
RSS