作者 ,译者
AI前线导读:
如何优化SQL连接是数据库社区数十年来一直在研究的一个大问题。近日,伯克利RiseLab公布的一项研究表明,深度强化学习可以被成功地应用在优化SQL连接上。对于大型的连接,这项技术的速度比传统动态规划快上10倍,比穷举快上10000倍。这篇文章将介绍SQL连接问题以及这项强大的优化技术,更多详细内容可以参看论文”Learning to Optimize Join Queries With Deep Reinforcement Learning“(链接在文末)。
数据库社区已经针对SQL查询优化问题进行了近40年的研究,可以追溯到System R的动态规划方法。查询优化的核心是连接排序问题。尽管这个问题由来已久,但仍然有很多研究项目尝试更好地理解多连接查询中的连接优化器的性能,或者解决在企业级“数据湖泊”中无处不在的大型连接查询问题。
在我们的论文中,我们表明了如何通过深度强化学习技术来攻克这个已经存在了数十年的挑战。我们将连接排序问题表示为马尔可夫决策过程(MDP),然后构建了一个使用深度Q网络(DQN)的优化器,用来有效地对连接进行排序。我们基于Join Order Benchmark(最近提出的工作负载,专门用于压力测试连接优化)对我们的方法进行了评估。我们只使用了适量的训练数据,基于强化学习的深度优化器的执行计划成本比所有我们能想到的成本模型最优解决方案改进了2倍,比下一个最好的启发式改进最多可达3倍——所有这些都在计划的延迟范围,比动态规划快10倍,比穷举快10000倍。
背景:连接排序
为什么强化学习是解决连接排序问题的好方法?要回答这个问题,先让我们回顾一下传统的动态规划(DP)方法。
假设一个数据库包含三张表:Employees、Salaries和Taxes。下面这个查询用于找出“所有Manager 1员工的总税额”:
SELECT SUM(S.salary * T.rate)
FROM Employees as E, Salaries as S, Taxes as T
WHERE E.position = S.position AND
T.country = S.country AND
E.position = ‘Manager 1’这个查询包含了三个关系连接。在下面的示例中,我们使用J(R)表示访问基本关系R的成本,使用J(T1,T2)表示连接T1和T2的成本。为简单起见,我们假设了一个访问方法,一个连接方法和一个对称连接成本(即J(T1,T2)=J(T2,T1))。
经典的“left-deep”DP方法首先计算访问三个基本关系的最佳成本,我们把结果放在一张表中:
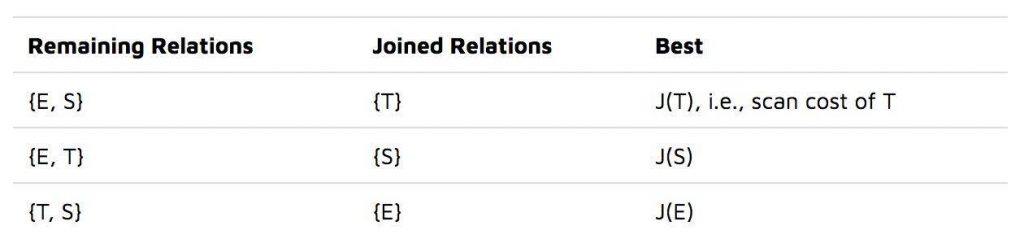
然后,它基于这些信息枚举所有二元关系。例如,在计算{E,S}连接的最佳成本时,它会查找先前相关的计算结果:
Best({E, S}) = Best({E}) + Best({S}) + J({E}, S)
这样就得到了新的一行:

这个算法遍历其他二元关系集,最终找到连接所有三张表的最佳成本。这需要在二元关系和基本关系的所有可能“left-deep”组合中取最小值:

这就是动态规划方法。请注意,J的第二个操作数(关系的右边部分)始终是基本关系,而左边可以是中间连接结果(因此叫作“left-deep”)。这个算法的空间复杂度和时间复杂度将随着关系的数量增加呈指数级增长,这就是为什么它通常只被用于10-15个关系的连接查询。
通过强化学习进行连接排序
我们的主要想法如下:不使用如上所示的动态规划来解决连接排序问题,而是将问题表示为马尔可夫决策过程(MDP),并使用强化学习(RL)来解决它,这是一种用于解决MDP的一般性随机优化器。
首先,我们将连接排序表示为MDP:
- 状态,G:需要连接的剩余关系。
- 动作,c:剩余关系之外的有效连接。
- 下一个状态,G’:这是旧的“剩余关系”的集合,移除了两个关系,并添加了它们的结果连接。
- 奖励,J:新连接的估算成本。
可以简单地表示成(G, c, G’, J) 。
我们使用Q-learning(一种流行的RL技术)来解决连接排序MDP。我们定义了Q函数Q(G,c),它直观地描述了每个连接的长期成本:我们在当前连接决策之后对所有后续连接采取最佳操作的累积成本。
Q(G, c) = J(c) + \min_{c’} Q(G’, c’)
请注意,如果我们可以访问真正的Q函数,就可以进行贪婪的连接排序:
算法1
- 从初始查询图开始;
- 找到Q(G,c)最低的连接;
- 更新查询图并重复。
根据贝尔曼的最优性原则,我们的这个算法可证明是最优的。这个算法令人着迷的地方在于它的计算复杂度为O(n^3),虽然仍然很高,但却远低于动态规划的指数级运行时复杂度。
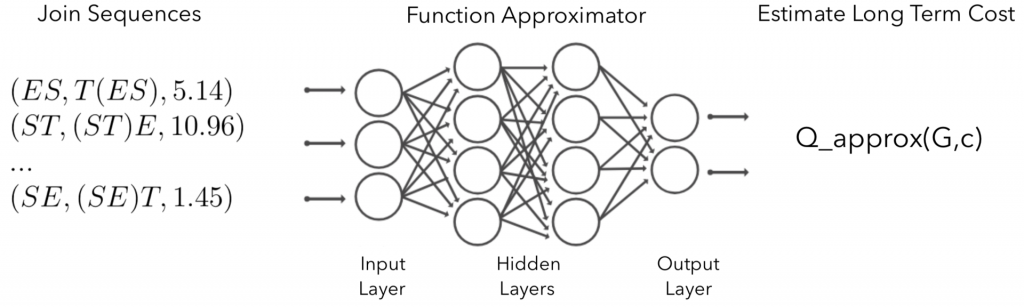
图1:使用神经网络逼近Q函数。输出的意思是“如果我们在当前查询图G上进行连接c,那么最小化长期连接计划成本是多少?”
当然,实际上我们无法访问真正的Q函数,需要对其进行近似。为此,我们使用神经网络(NN)来学习Q函数,并称其为深度Q网络(DQN)。这项技术与用于学习Atari游戏专家级玩家能力的技术如出一辙。总而言之,我们的目标是训练一个神经网络,它接收(G,c)作为输入,并输出估算的Q(G,c),见图1。
深度强化学习优化器DQ
现在介绍我们的深度强化学习优化器DQ。
数据采集。要学习Q函数,我们首先需要观察过去的执行数据。DQ可以接受来自任何底层优化器的一系列(G,c,G’,J)。例如,我们可以运行经典的left-deep动态规划(如背景部分所示),并从DP表中计算出一系列“连接轨迹”。完整轨迹中的元组看起来像是(G,c,G’,J)=({E,S,T}, join(S,T), {E,ST},110),它代表从初始查询图(状态)开始并将S和T连接在一起(动作)的步骤。
我们已经使用J表示连接的估算成本,但如果数据时从真实的数据库执行收集而来,我们也可以使用实际的运行时。
状态和动作的特征化。由于使用神经网络来表示Q(G,c),我们需要将状态G和动作c作为固定长度的特征向量馈送到网络中。DQ的特征化方案非常简单:我们使用1-hot向量来编码(1)查询图中存在的所有属性的集合,包括模式中的所有属性,(2)连接左侧的参与属性, (3)连接右侧的属性。如图2所示。

图2:查询及其相应的特征化。我们假设一个包含Employees、Positions和Salaries三张表的数据库。图中显示了部分连接和完全连接。(G,c)的最终特征向量是A_G(查询图的属性)、A_L(左侧的属性)和A_R(右侧的属性)的串联。
虽然这个方案非常简单,但我们发现它具有足够的表现力。需要注意的是,我们的方案(和学习的网络)假设的是一个固定的数据库,因为它需要知道确切的属性集和表集。
神经网络训练和规划。默认情况下,DQ使用简单的两层全连接网络,并使用标准随机梯度下降进行训练。在完成训练后,DQ可以接受纯文本的SQL查询语句,将其解析为抽象语法树,对树进行特征化,并在每次候选连接获得评分时调用神经网络(也就是在算法1的步骤2中调用神经网络) )。最后,可以使用来自实际执行的反馈定期重新调整DQ。
评估
为了评估DQ,我们使用了最近发布的Join Order Benchmark(JOB)。这个数据库由来自IMDB的21个表组成,并提供了33个查询模板和113个查询。查询中的连接关系大小范围为5到15个。当连接关系的数量不超过10个时,DQ从穷举中收集训练数据。
比较。我们与几个启发式优化器(QuickPick和KBZ)以及经典动态规划(left-deep、right-deep、zig-zag)进行比较。我们对每个优化器生成的计划进行评分,并与最优计划(我们通过穷举获得)进行比较。
成本模型。随着新硬件的创新(例如NVRAM)和向无服务器RDBMS架构(例如Amazon Aurora Serverless)的转变,我们期望看到大量新的查询成本模型可以捕获不同的硬件特征。为了显示基于学习的优化器可以适应不同的环境,我们设计了3个成本模型:
- Cost Model 1(Index Mostly):模拟内存数据库并鼓励使用索引连接。
- Cost Model 2(Hybrid Hash):仅考虑具有内存预算的散列连接和嵌套循环连接。
- Cost Model 3(Hash Reuse):考虑重用已构建的散列表。
从CM1到CM3,成本表现出更多的非线性,向静态策略提出了挑战。
我们进行了4轮交叉验证,确保仅对未出现在训练工作负载中的查询进行DQ评估(对于每种情况,我们在80个查询上训练并测试其中的33个)。我们计算查询的平均次优性,即“成本(算法计划)/成本(最佳计划)”,这个数字越低越好。例如,对Const Model 1,DQ平均距离最佳计划1.32倍。结果如图3所示。
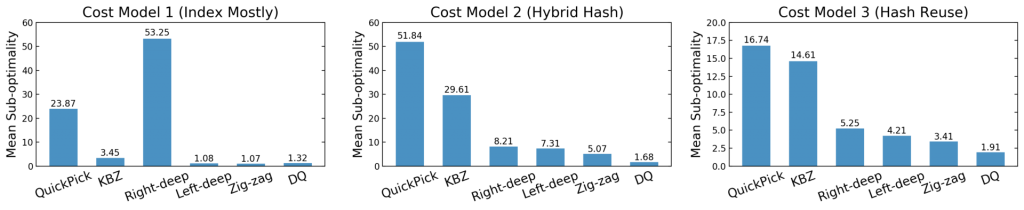
图3:不同成本模型的平均计划次优性。
在所有成本模型中,DQ在没有指数结构的先验知识的前提下可以与最优解决方案一比高下。对于固定的动态规划,情况并非如此:例如,left-deep在CM1中产生了良好的计划(鼓励使用索引连接),但在CM2和CM3中效果没有那么好。同样,right-deep计划在CM1中没有竞争力,但如果使用CM2或CM3,right-deep计划突然变得不那么糟糕。需要注意的是,基于学习的优化器比手动设计的算法更强大,可以适应工作负载、数据或成本模型的变化。
此外,DQ以比传统动态规划快得多的速度产生了良好的计划(图4)。
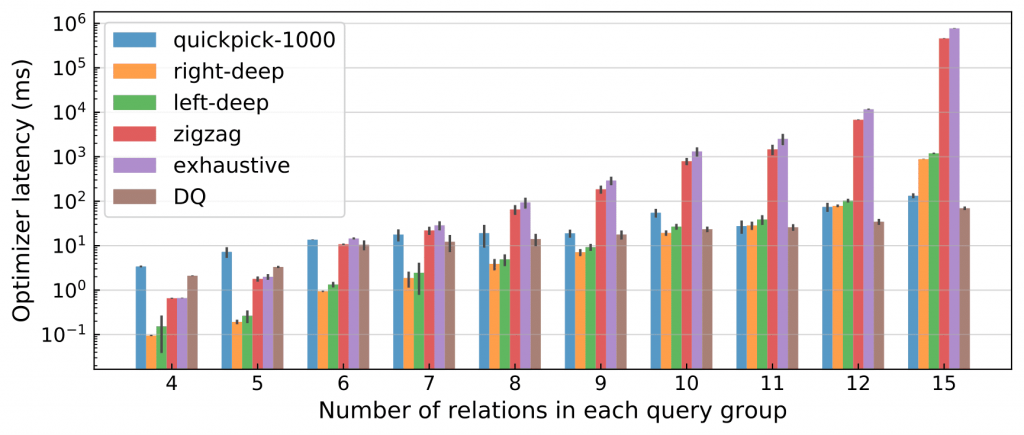
图4:所有113个JOB查询的优化器延迟,按查询中的关系数量进行分组。误差棒表示平均值附近的±标准偏差。共进行了5次试验。
在大型连接机制中,DQ实现了极大的加速:对于最大的连接,DQ的速度是穷举的10000倍,比zig-zag快1000倍,比left-deep和right-deep枚举快10倍。性能增益主要来自神经网络提供的丰富的批处理机会——对于单个迭代中所有的候选连接,DQ针对整个批处理调用一次NN。我们相信,对于这样一个学习优化器来说,这是一个意义深远的性能改进:对于更大的查询或运行在专用加速器(例如GPU、TPU)上时,它将表现出更大的优势。
概要
我们认为深度强化学习非常适合用来解决连接排序问题。深度强化学习使用数据驱动方法来调整针对特定数据集和工作负载的查询计划,并观察连接成本,而不是使用固定的启发式。为了选择查询计划,DQ使用了能够在训练时编对态规划表的压缩版本进行编码的神经网络。
DQ只是冰山一角,在数据库社区存在激烈的争论,围绕着如何将更多的学习(或者说是数据适应性)纳入到现有系统中。我们希望我们的工作是实现更智能的查询优化器的第一步。有关详细信息,请参阅我们的Arxiv论文。
Arxiv论文链接:https://arxiv.org/abs/1808.03196
英文原文:https://rise.cs.berkeley.edu/blog/sql-query-optimization-meets-deep-reinforcement-learning/
转自 http://www.infoq.com/cn/articles/sql-query-optimization-meets-deep-reinforcement-learning
 Linuxeden开源社区
Linuxeden开源社区