前言
我最近一直在公司做检索性能优化。当我看到这个算法之前,我也不认为我负责的检索系统性能还有改进的余地。但是这个算法确实太牛掰了,足足让服务性能提高50%,我不得不和大家分享一下。其实前一段时间的博客中也写到过这个算法,只是没有细讲,今天我准备把它单独拎出来,说道说道。说实话,本人数学功底一般,算法证明不是我强项,所以文中的证明只是我在论文作者的基础上加入了自己的思考方法,并且还没有完全证明出来,请大家见谅 ! 欢迎爱思考的小伙伴进行补充。我只要达到抛砖引玉的作用,就知足了。
回归正题,我们的检索服务中用到了最小编辑距离算法,这个算法本身是平方量级的时间复杂度,并且很少人在帖子中提到小于这个复杂度的算法。但是我无意中发现了另外一个更牛的算法:列划分算法,使得这个本就很牛的算法性能直接提高一倍。接下来进入正题。
列划分算法
这个算法比较难理解,出自如下论文:《Theoretical and empirical comparisons of approximate string matching algorithms》。In Proceedings of the 3rd Annual Symposium on Combinatorial Pattern Matching, number 664 in Lecture Notes in Computer Science, pages 175~184. Springer-Verlag, 1992。Author:WI Chang ,J Lampe。所以有必要先给大家普及一些共识。
编辑矩阵 最小编辑距离在计算过程中使用动态规划算法计算的那个矩阵,了解这个算法的都懂,我不赘述。但是我们的编辑矩阵有个特点:第一行都是0,这么做的好处是:只要文本串T中的任意一个子序列与模式串P的编辑距离小于某个固定的数值,就会被发现。
给大伙一个样例,文本串T=annealing,模式串P=annual:

注意,第一行都是0,这是与传统最小编辑距离的最大区别,其余的动归方程完全相同。
对角线法则 编辑矩阵沿着右下方对角线方向数值非递减,并且至多相差1。
行列法则 每行每列相邻两个数至多相差1。
观察编辑距离矩阵,我们发现如下事实:每一列是由若干段连续数字组成。所以我们把编辑矩阵的每一列划分成若干连续序列,如下图所示:

红色框中就是一个一个的序列,序列内部连续。
序列-δ 定义 对于编辑矩阵的每一个元素D[j][i] (j是行,i是列),若 j – D[j][i] = δ,我们就说D[j][i]属于i列上的 序列-δ,我们还观察到随着j增大,j – D[j][i]是非递减的。如下图所示:

序列-δ终止位置 每个序列都会有起始和终止位置。序列-δ的终止位置为j,如果j是序列-δ的最小横坐标,并且满足D[j+1][i]属于序列-ε,并且ε>δ(即j+1-D[j+1][i]>δ)。
长度为0的序列 我们发现如果按照如上定义,每一列上δ的值并不一定连续,总是或有或无的缺少一个数值。所以我们定义长度为0的序列:当D[j+1][i] < D[j][i]时,我们就在序列-δ和序列-(δ+2)之间人为插入一个长度为0的序列-(δ+1)。如下图所示:

所以,我们按照这个定义,就可以对编辑矩阵的每列进行一个划分,划分的每一段都是一串连续数字。
说了这么多,这个定义有什么用呢?假若,我们每次都能根据前一列的列划分情况直接推导出后一列的列划分情况,那么就可以省去好多计算,毕竟每一个划分中的每一段的数字都是连续的,这就暗示我们可以直接用一个常数时间的加法直接得到某一个编辑矩阵的元素值,而不用使用最小编辑距离的动态规划算法去计算。
接下来的重点来了,我们介绍这个推导公式,请打起十二分精神!我们按照序列-δ长度是否为0来介绍这个推论。由于其中一个推论文字描述太繁琐,不容易理解,所以我画了个图:
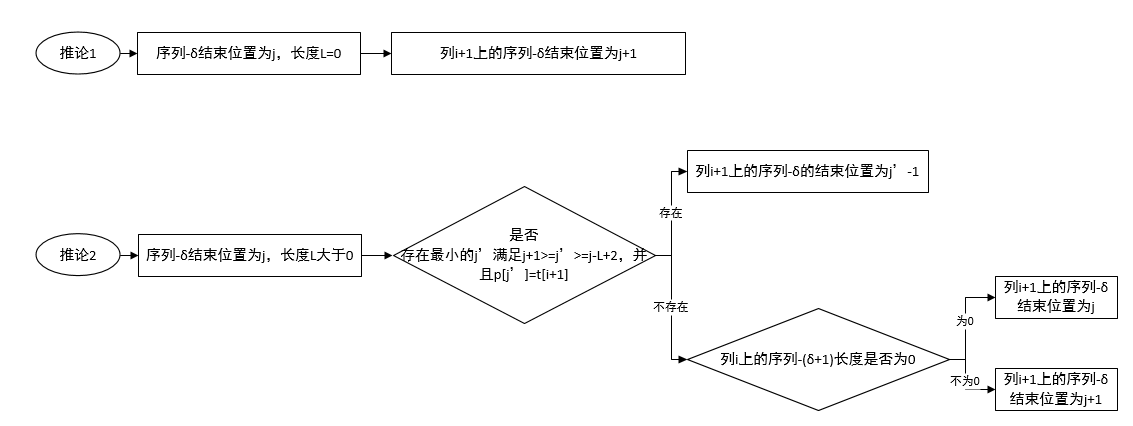
接下来烧脑开始。
推论1:如果列i上长度为0的 序列-δ 的结束位置为j,则列i+1上的 序列-δ 的结束位置为 j+1。
证明 :由推论前提我们知道 δ = j – D[j][i] + 1 (想想前面说的δ值不连续,我们就人为插入一个中间值,只不过长度为0)。
我们观察编辑矩阵就会发现如下两个事实:
- 事实1:D[j+1][i+1] = D[j][i] ( 别问为什么, 自己观察, 看看是不是都这样, 其实可以用反证法,我们就不证明了)。
- 事实2:D[j+2][i+1] <= D[j][i]。
通过事实1,我们知道D[j+1][i+1]确实属于 序列-δ,因为 j + 1 – D[j+1][i+1] = j + 1 – D[j][i] = δ。
通过事实2,我们知道列i+1上的序列δ,终止位置为j+1。
所以推论1证明结束。
推论2: 文字描述略,请看图
证明 :
- 设这个序列长度为L,除了每列的第一个序列外,其余序列的其余位置均是当前的编辑距离小于等于该列上一个位置的编辑距离:即D[j-L+1][i]<=D[j-L][i],所以,我们可以推出:D[j-L+1][i] <= D[j-L][i];
- 再根据编辑矩阵对角线非递减我们知道,D[j-L+1][i+1] >= D[j-L][i];
综上两点我们得到如下大小关系:D[j-L+1][i+1] >= D[j-L+1][i]。
此外我们知道我们当前列的序列-δ截止位置为j,也意味着D[j+1][i] <= D[j][i],同样根据对角线法则,我们得出D[j+2][i+1] <= D[j+1][i] + 1 <= D[j][i] + 1。
接下来到了最精彩的一步,我们知道列i当前序列-δ内的值是连续的,如果起始编辑距离为A,那么终止编辑距离为A+L-1。
而由我们的推导可以发现:D[j-L+1][i+1] >= A,D[j+2][i+1] <= (A+L-1) + 1 = A+L,而之间跨越的长度为 (j+2)-(j-L+1)+1= L+2。 我们可以推出列i+1上从行j-L+1到行j+2之间的序列一定不连续,否则D[j+2][i+1] >= A+L+2-1= A+L+1,与我们先前的推导矛盾。所以,在j-L+1和j+2之间一定有一个列终止,这样才能消去一个序号。
此外我们还有一个疑问,列i+1上的序列-δ结束位置一定在j-L+1和j+1之间么?我们要证明这个事。
证明 :
因为δ=j-D[j][i]=j-L+1-D[j-L+1][i]>=j-L+1-D[j-L+1][i+1],即列i+1上的 序列-δ的结束位置一定在j-L+1或者之后;
由于j+1-D[j+1][i]>δ,根据对角线法则D[j+2][i+1] <= D[j+1][i]+1,有j+2-D[j+2][i+1]>=j+2-(D[j+1][i]+1)=j+1-D[j+1][i] > δ, 固列i+1上的序列-δ的终止位置一定在j+2之前,即j-L+1到j+1之间。
后面推论2的分情况讨论,我一个也没证明出来,作者在论文中轻飘飘的一句话“后面很好证明,他就不去证明了”,但是却消耗了我所有脑细胞。所以,如果哪位小伙伴把推论2剩下的内容证明出来了,欢迎给我留言,我也学习学习。
这个算法的时间复杂度是多少呢?作者用启发式的方法证明了算法的复杂度约为$ O(mn/sqrt[2]{b}) $,其中b是字符集大小。
代码实现
接下来说一下代码实现,给出我总结出来的步骤,否则很容易踩坑。
- 编辑矩阵第一列,肯定只有一个序列。
- 每次遍历前一列的所有序列,根据推论1和推论2计算后一列的划分情况。
- 如果前一列遍历完毕,但是下一列还有剩余的元素没有划分。没关系,下一列剩下的元素都归为一个新的序列。
- 预处理一个表,表中记录T中的每个字符在P中的位置。可以直接用哈希算法(最好直接ascii码)进行定位,如果位置不唯一,可以拉链。进行列划分计算时,从前往后遍历那一链上的位置,直到找到第一个符合条件的,速度出奇的快。尽可能少使用或者不要使用map进行定位,测试发现相当慢。
接下来做最不愿意做的事:贴一个代码,很丑。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
|
inline int loc(int find[][200], int *len, int ch, int pos) {
for(int i = 0; i < len[ch]; ++i) {
if(find[ch][i] >= pos) return find[ch][i];
}
return –1;
}
int new_column_partition(char *p, char *t) {
int len_p = strlen(p);
int len_t = strlen(t);
int find[26][200];
int len[26] = {0};
int part[200]; //记录每一个序列的结束位置
//生成loc表,用来快速查询
for(int i = 0; i < len_p; ++i) {
find[p[i] – ‘a’][len[p[i] – ‘a’]++] = i + 1;
}
int pre_cn = 0, next_cn = 1, min_v = len_p;
part[0] = len_p;
for(int i = 0; i < len_t; ++i) {
//前一列partition数
pre_cn = next_cn;
next_cn = 0;
int l = part[0] + 1;
int b = 1;
int e = l;
int tmp;
int tmp_value = 0;
int pre_v = part[0];
//前一列第0个partition长度肯定>=1
if(len[t[i] – ‘a’] >0 && (tmp = loc(find, len, t[i] – ‘a’, b)) != –1 && tmp <= e) {
part[next_cn++] = tmp – 1;
} else if(pre_cn >= 2 && part[1] – part[0] != 0){
part[next_cn++] = part[0] + 1;
} else {
part[next_cn++] = part[0];
}
//每列第一个partition尾值
tmp_value = part[0];
//遍历前一列剩下的partition
for(int j = 1; j < pre_cn && part[next_cn – 1] < len_p; ++j) {
int x = part[j], y = pre_v;
pre_v = part[j];
l = x – y;
if(l == 0) {
part[next_cn++] = x + 1;
} else {
b = x – l + 2;
e = x + 1;
if(b <= len_p && len[t[i] – ‘a’] > 0 && (tmp = loc(find, len, t[i] – ‘a’, b)) != –1 && tmp <= e) {
part[next_cn++] = tmp – 1;
} else if(j + 1 < pre_cn && part[j + 1] – x != 0) {
part[next_cn++] = x + 1;
} else {
part[next_cn++] = x;
}
}
l = part[j] – part[j – 1];
if(l == 0) {
//新得到的partition长度为0,那么下一个partition的起始值比上一个partition尾值少1
tmp_value -= 1;
} else {
tmp_value += l – 1;
}
}
if(part[next_cn – 1] != len_p) {
part[next_cn++] = len_p;
tmp_value += len_p – part[next_cn – 2] – 1;
if(tmp_value < min_v) {
min_v = tmp_value;
}
} else {
min_v = min_v < tmp_value ? min_v : tmp_value;
}
}
return min_v;
}
|
结语
这个算法应用到线上之后,效果非常明显,如下对比。
- 优化前CPU:
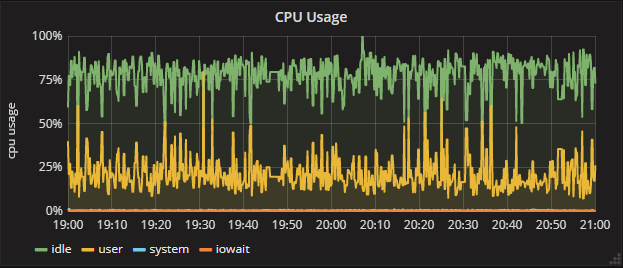
- 优化后CPU:
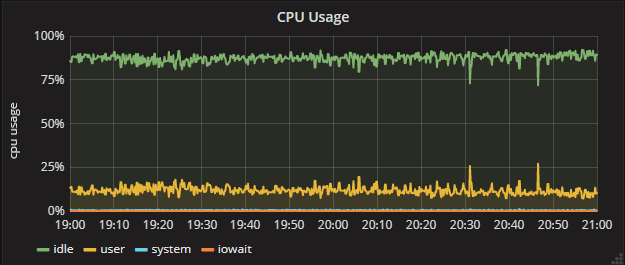
能力有限,证明不充分,有兴趣的小果伴可以直接去看原版论文,欢迎交流,共同进步。
转自 http://blog.jobbole.com/114324/
 Linuxeden开源社区
Linuxeden开源社区